class: center, middle, inverse, title-slide # Topic 7: Global Measures of Spatial Autocorrelation ### Dr. Kam Tin Seong<br/>Assoc. Professor of Information Systems ### School of Computing and Information Systems,<br/>Singapore Management University ### 2020-5-1 (updated: 2021-06-21) --- ## Content .large[ - What is Spatial Autocorrelation - Measures of Global Spatial Autocorrelation - Measures of Global High/Low Clustering ] --- # What is Spatial Autocorrelation .large[ - Toble's First Law of Geography - Spatial Dependency - Spatial Autocorrelation - Positive autocorrelation - Negative autocorrelation ] --- ## Tobler’s First law of Geography .center[ ### Everything is related to everything else,<br/> but near things are more related than distant things. ]. 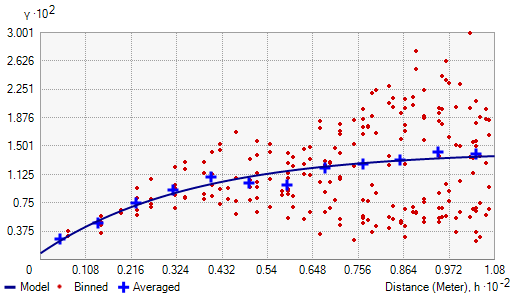.pull-left[ .large[ The foundation of the fundamental concepts of: - spatial dependence, and - spatial autocorrelation ]] .pull-right[ ] .small[[Reference: A Computer Movie Simulating Urban Growth in the Detroit Region](http://www.geog.ucsb.edu/~tobler/publications/pdf_docs/A-Computer-Movie.pdf) ] --- ## Spatial Dependency .pull-left[ .large[ - Spatial dependence is the spatial relationship of variable values (for themes defined over space, such as rainfall) or locations (for themes defined as objects, such as cities). - Spatial dependence is measured as the existence of statistical dependence in a collection of random variables, each of which is associated with a different geographical location. ]] .pull-right[ ] --- ## Spatial Autocorrelation .large[ - Spatial autocorrelation is the term used to describe the presence of systematic spatial variation in a variable. - The variable can assume values either: - at any point on a continuous surface (such as land use type or annual precipitation levels in a region); - at a set of fixed sites located within a region (such as prices at a set of retail outlets); or - across a set of areas that subdivide a region (such as the count or proportion of households with two or more cars in a set of Census tracts that divide an urban region).] .center[ ] --- ## 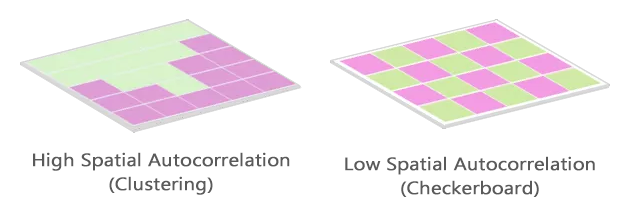Positive Spatial Autocorrelation .pull-left[ .large[ - Clustering - like values tend to be in similar locations. - Neighbours are similar - more alike than they would be under spatial randomness. - Compatible with diffusion - but not necessary caused by diffusion. ]] .pull-right[ ] --- ## Negative Spatial Autocorrelation .pull-left[ .large[ - Checkerboard patterns - “opposite” of clustering - Neighbours are dissimilar - more dissimilar than they would be under spatial randomness - Compatible to competition - but not necessary competition ]] .pull-right[ ] --- # Measures of Global Spatial Autocorrelation .vlarge[ - Moran’s I - Geary's c ] --- ## Measures of Global Spatial Autocorrelation: Moran’s I .large[Describe how features differ from the values in the study area as a whole ] .center[ ] .large[ - 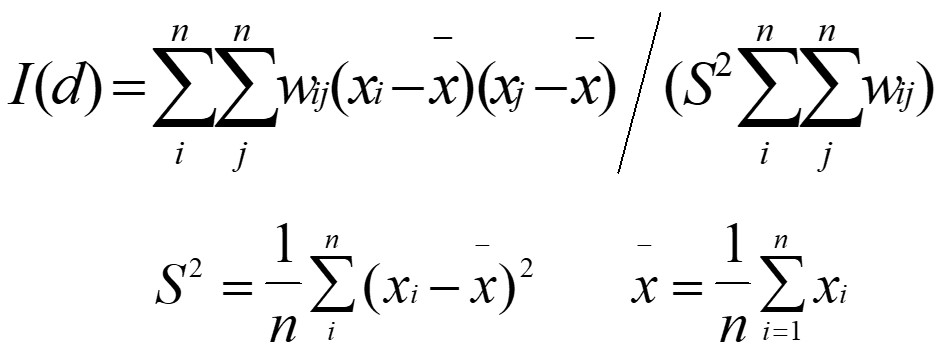Moran I (Z value) is: - positive (I>0): Clustered, observations tend to be similar; - negative(I<0): Dispersed, observations tend to be dissimilar; - approximately zero: observations are arranged randomly over space.] --- ## Measures of Global Spatial Autocorrelation: Geary's c .large[ - Describing how features differ from their immediate neighbours] .center[ ] .large[ - 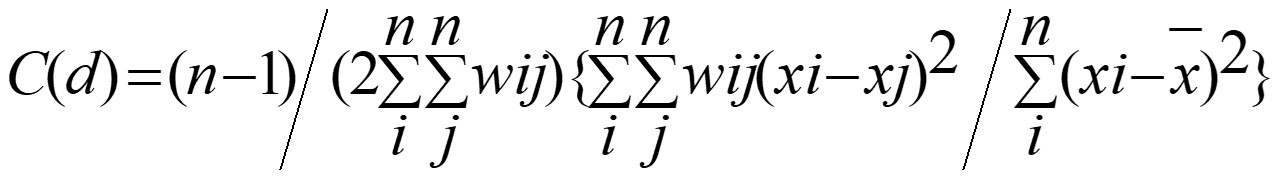Geary c (Z value) is: - Large c value (>1) : Dispersed, observations tend to be dissimilar; - Small c value (<1) : Clustered, observations tend to be similar; - c = 1: observations are arranged randomly over space. ] --- ## Relationship of Moran’s I and Geary’s C .large[ - C approaches 0 and I approaches 1 when similar values are clustered. - C approaches 3 and I approaches -1 when dissimilar values tend to cluster. High values of C measures correspond to low values of I. - So the two measures are inversely related. ] --- ## z-score and p-value explained .pull-left[ .large[ - Statistically, we select the confident interval such as 95% => alpha value = 0.05. - Reject the Null hypothesis (H0) if p-value is smaller than alpha value. - Failed to reject the Null Hypothesis (H0) if p-value is greater than alpha value. 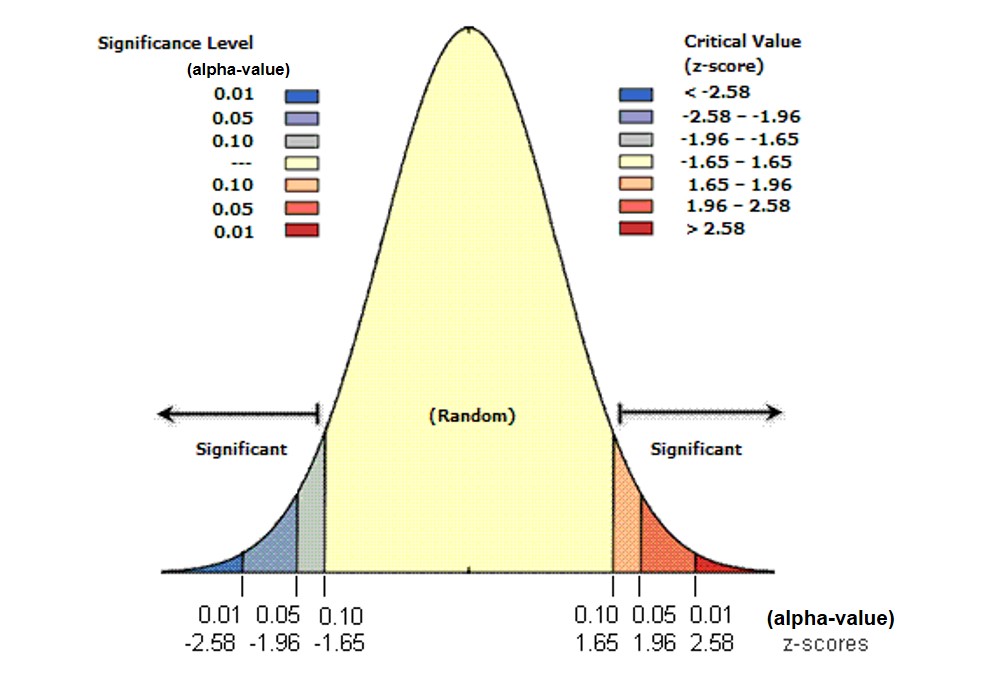]] .pull-right[ ] .small[Reference: Confidence Interval or P-Value? https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2689604/] --- ## Spatial Randomness .large[ The Null Hypothesis: - Observed spatial pattern of values is equally likely as any other spatial pattern. - Values at one location do not depend on values at other (neighbouring) locations. - Under spatial randomness, the location of values may be altered without affecting the information content of the data.] --- ## What if my data violate the assumptions? .large[ - If you doubt that the assumptions of Moran’s I are true (normality and randomization), we can use a Monte Carlo simulation. - Simulate Moran’s I n times under the assumption of no spatial pattern, - Assigning all regions the mean value - Calculate Moran’s I, - Compare actual value of Moran’s I to randomly simulated distribution to obtain p-value (pseudo significance). ] --- # Measures of Global High/Low Clustering .vlarge[ - Getis-Ord Global G ] --- ## Measures of Global High/Low Clustering: Getis-Ord Global G .large[ - The G(d)G(d)G(d) statistic is concerned with the overall concentration or lack of concentration in all pairs that are neighbours given the definition of neighbouring areas. 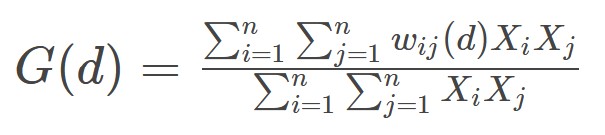- The variable must contain only positive values to be used.] .center[ ] .small[ Source: Getis, A., & Ord, K. (1992). ["The Analysis of Spatial Association by Use of Distance Statistics"](https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1538-4632.1992.tb00261.x). *Geographical Analysis*, 24, 189–206. ] --- ## Interpretation of Getis-Ord Global G .large[ - The p-value is not statistically significant. - You cannot reject the null hypothesis. It is possible that the spatial distribution of feature attribute values is the result of random spatial processes. Said another way, the observed spatial pattern of values could be one of many possible versions of complete spatial randomness. - The p-value is **statistically significant**, and the z-score is **positive**. - You can reject the null hypothesis. The spatial distribution of high values in the dataset is more spatially clustered than would be expected if underlying spatial processes were truly random. - The p-value is **statistically significant**, and the z-score is **negative**. - You can reject the null hypothesis. The spatial distribution of low values in the dataset is more spatially clustered than would be expected if underlying spatial processes were truly random. ] --- ## References .large[ - Moran, P. A. P. (1950). ["Notes on Continuous Stochastic Phenomena"](https://www-jstor-org.libproxy.smu.edu.sg/stable/2332142?seq=1#metadata_info_tab_contents). Biometrika. 37 (1): 17–23. - Geary, R.C. (1954) ["The Contiguity Ratio and Statistical Mapping"](https://www-jstor-org.libproxy.smu.edu.sg/stable/2986645?sid=primo&origin=crossref&seq=1#metadata_info_tab_contents). *The Incorporated Statistician*, Vol. 5, No. 3, pp. 115-127. - [Moran's I](https://en.wikipedia.org/wiki/Moran%27s_I) - [Geary's c](https://en.wikipedia.org/wiki/Geary%27s_C) - Getis, A., & Ord, K. (1992). ["The Analysis of Spatial Association by Use of Distance Statistics"](https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1538-4632.1992.tb00261.x). *Geographical Analysis*, 24, 189–206. ]